[cs231n] Lecture 2 | Image Classification

Stanford의 유명 강의인 cs231n을 수강하고 정리한 글이다.

해당 강의는 유튜브에서 무료로 볼 수 있다.

 

2강 -

https://www.youtube.com/watch?v=OoUX-nOEjG0&list=PLC1qU-LWwrF64f4QKQT-Vg5Wr4qEE1Zxk&index=3

 

오늘은 2강인 Image Classification에 대해 정리해 보려 한다.

 

 

✏️ Image Classification

---

• Image Classification은 어떤 사진에 대해 정해진 Lables 중 하나를 고르는 것이다.
• 우선 컴퓨터는 우리가 보는 것처럼 사진을 보지 않는다. 그저 수많은 숫자의 배열로서 본다.

• 위와 같은 고양이 사진을 아래와 같은 숫자로 보는 것
• 근데 이렇게 숫자로 보면 각도, 조명 등에 따라 숫자가 바뀐다. 이러한 조건을 모두 고려하는 프로그래밍은 사실상 없다. (강의에서는 기적에 가깝다고 구술함)
• 하지만 일부 제한된 환경에서는 거의 사람과 비슷한 정확도를 낸다고 한다.

 

✏️ Image Classification Algorithm

---

• Image Classification 의 접근법 두개가 있다.
• 하나는 Corner와 Edge를 이용하여 특정한 규칙 집합을 만드는 방법이다.
  • 결론적으로, 별로이다. 왜냐하면
  • 첫 째, Robust(강인) 하지 않다. 이는 이미지가 달라지면 적용이 어려움을 뜻한다.
  • 둘 째, 모든 객체에 대해 만들어야 한다. 위 방법은 간단한 예시를 들자면 고양이의 간단한 모양의 스케치를 해놓고, 이렇게 생기면 고양이다! 라고 하는 방법인데 그러면 나머지 객체들도 똑같이 그려놔야 가능하다. 즉, 비효율적이며, 완전하지 않다.
• 이를 해결하기 위해 Data-Driven Approach (데이터 중심 접근법) 이 존재한다.
  • 이 방법을 위해서는 다양한 객체의 이미지를 수집해야하지기에 어느정도 노가다이지만, 인터넷에 이미 양질의 데이터셋이 많이 존재한다.
  • 이 데이터셋들을 ML Classifier를 학습시키는데 사용할 수 있다.
• 자 이제 개와 고양이를 분류하는 API를 만들어보자, 데이터 중심 접근법을 사용한다면 두개의 API 함수가 필요할 것
  • Train 함수
    • Input : 이미지와 레이블
    • Output : 모델
  • Predict
    • Input : 모델
    • Output : 이미지의 예측값

 

✏️ Nearest Neighbor

---

• 복잡한 알고리즘 이전에 간단한 Nearest Neighbor이라는 알고리즘이 있다.
• NN 알고리즘은?
  • 학습 단계에서 그저 데이터를 기억만 한다. (수업에서는 외운다고 비유)
  • 예측 단계에서 새로운 이미지가 들어오면 기존 데이터와 비슷한 곳으로 분류한다.
• NN 알고리즘으로 CIFAR-10에 있는 10가지 클래스를 분류해보았다.
• 결과는 비슷하게는 나오지만 거의 틀린다. (수업에서는 첫째 행은 맞았고 나머지는 틀렸다.)
• 그래도 굉장히 간단한 것에 비하면 나쁘진 않다. 그렇다면 사진이 비슷한지 어떻게 알아낼까?

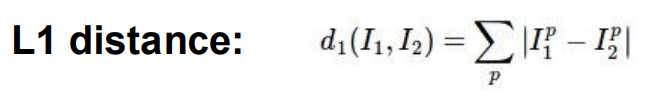
• L1 distance (Manhatten Distance) 를 이용한다. 이는 배열의 각각 값을 빼준 것의 절대값을 다 더해준 값이 된다.

• 결과로 하나의 수가 등장하는데, 이는 두 이미지의 거리(차이)이다.
• 이를 통해 해당 사진이 어떤 레이블과 가장 가까운지를 판단할 수 있다.
• Q. NN알고리즘에서 N개의 데이터가 있으면, 학습과 예측에 얼마의 시간이 걸릴까?
  • 학습 과정은 하는게 없다. 수업에서는 '외운다'라고 예시를 들었지만, 컴퓨터는 외우는데 시간이 걸리지 않는다. 즉, O(1)
  • 예측은 얼마나 걸릴까? (Test Image는 1개, 예측 1번일 때)
    • 예측에서 N개의 데이터가 있다면 test image에서 N개를 빼주면서 어떤 것이 가장 차이가 적은지 찾는다.
    • 코드로 보면, for문 하나가 필요
    • O(N)의 시간이 걸린다.
  • 그럼 여기서 문제가 생긴다. 우리는 학습이 얼마나 걸리던지 예측이 빠른 모델을 원한다. 그런데 이 모델은 학습이 빠르고 예측이 느리다..
• 또한, NN의 Decision Region 살펴보자

• 초록색 영역에 노란색 점 하나가 있는데 노란색 영역을 가지고 있는 불편한 결과가 나올 수 있다. 이는 원래 초록색으로 분류 되어야할 점이 노란색으로 분류될 수도 있다. (가장 근접한 이웃 점의 색을 따라가기 때문)

 

✏️ K-Nearest Neighbor

---

• 그래서 나온 방법이 K-Nearest Neighbor이다. 비슷한 알고리즘이지만, 주변 K개를 봤을 때, 가장 비슷한 것을 고른다.
• KNN으로 사진 분류를 진행했을때, 멀리서 보면 비슷한 사진을 골랐지만, 가까이서 봤을 때 완전히 틀린 사진을 골랐다.
• 이번엔 거리 구하는 공식을 바꿔보자, 기존의 L1이 아닌 L2(Euclidean)을 사용할 수도 있다.

• 수업에서는 특징 벡터가 실질적인 의미를 가진다면 L1 Distance가 더 잘 어울릴 수 있고, 그 반대의 경우는 L2 Distance가 더 잘 어울릴 수 있다고 했다. 또한, L1은 좌표축에 영향을 받는다. 하지만 L2는 좌표축에 영향을 받지 않는다. (아직 이것이 무엇을 의미하는지는 잘 모르겠다. 실습을 진행했을 때 L1은 각진? 느낌이었고, L2는 좀 더 부드러운 느낌이였다.)
• 그런데 여기서 또 궁금한 점이 생긴다. KNN에서 K값이랑 L1을 사용할 지 L2를 사용할 지는 누가 정해주는 걸까? 특별한 경우가 아니라면 우리가 찾아내야한다. 이러한 값을 Hyperparameter(초모수)라고 한다.
• 하이퍼파라미터를 제대로 맞추는 방법
  • 그냥 해본다 -> 특정 조건에만 적합한 하이퍼파라미터일 수 있음.
  • train과 test로 나누고 test에서 잘 반응하는 것으로 한다. -> test 데이터셋 말고 새로운게 들어오면?
  • train과 validation, test로 나눈다. -> train 데이터셋에서 훈련, validation 데이터셋에서 하이퍼파라미터를 조정, test에서 확인. 이렇게 하면 test 데이터셋은 우리의 데이터셋 안에 없는 아예 새로운 데이터가 된다.
• Cross-Validation 이라는 방식도 있다.

• 위 사진처럼 전체 데이터셋에서 특정 비율로 나누어 준다. (ex. 7:3)
• 3부분이 test가 된다. (마지막에 테스트해볼 데이터)
• 7 부분을 다시 나눈다. 사진에서는 5개로 나눴는데, 여기서 하나를 val(validation data)로 놓고 나머지를 train으로 놓는 방식을 반복하면서 하이퍼파라미터를 구하고, 그 평균으로 적절한 하이퍼파라미터를 구하는 것이다. 딥러닝에서는 자주 쓰이진 않는다고 한다.
• 또한, 같은 알고리즘이라고 (ex. KNN) 하이퍼파라미터까지 같지는 않다. 
• NN 방식은 아예 사용하지 않는다. 그 이유로 예측과정이 오래걸리고, 사진 사이의 거리값은 큰 의미가 없다. (실제로 측정해봐도 틀린값이 나온다.)
• 더 큰 문제는 차원이 넓어질 수록 필요한 데이터의 개수가 기하급수적으로 많아진다. 1차원일때 4개라면, 2차원 16개, 3차원 64개 등..

 

✏️ Linear Classification

---

• KNN은 사실 사용하지 않는다. 하지만 Linear Classification을 알기 위해서는 알아야한다.
• Linear Classification은 간단하지만 Neural Network와 CNN의 기반 알고리즘이다.
• NN(이제 Neural Network)는 레고블럭에 비유되는데, 교수님의 연구에 예를 들자면 이미지를 인식할때는 CNN을 사용하고 언어를 인식하기 위해서 RNN을 사용한다. 그냥 이 두개를 합치면 복잡한 문제도 해결이 되는 것이다.
• 다시 CIFAR-10 으로 돌아가보면 각 이미지는 32*32*3 픽셀이다.
• Linear classifier는 parametric(매개변수적) model의 가장 단순한 형태이다. parametric model에는 두개의 요소가 있다.
  • 입력 이미지 : X
  • 파라미터, 가중치 : W 혹은 세타
• 출력값은 10개의 숫자가 되며, 고양이의 점수가 높으면 고양이일 확률이 높다.
• 그렇다면 사진의 숫자들과 weight라는 변수를 넣으면 10개의 카테고리에 대한 score가 나온다. 즉, test 과정의 데이터셋이 필요가 없어진다.
• 가장 기본적인 형태의 함수는 f(x,W) = Wx + b이다.
• 이미지를 3072*1의 크기로 만든다. (32*32*3 이였으니) 이게 x가 된다.
• W는 3072*10 이다. (뒤에 10은 클래스의 개수이다.)
• 식에 따라 W의 첫번째 줄과 x를 곱하고, W의 두 번째 줄과 x를 곱하고 ... W의 열 번째 줄과 x를 곱해서 10개의 수를 구한다. 
• b는 bias이다. 편향값이 왜 필요할까, 만약 데이터셋에 고양이가 엄청 많고 강아지가 적다면 어떤 사진을 봤을 때 고양이일 확률이 더 크므로 고양이 점수에 추가를 해주는 것이다. 이는 예시에서는 10*1의 크기가 된다.

• 위 예시는 4pixel 3class 일 경우의 예이다. 

• Linear Classification 은 위와 같이 선형 결정경계를 그어주는 역할이다. 일차방정식이라고 생각하면 W가 기울기 b가 y절편 값에 해당하므로, 잘 조정해서 알맞은 사진들을 최대한 한 곳으로 몰아주는 것이 목표가 된다.

• 세 케이스 모두 직선 하나로 구분 할 수 없게 되어 있다. 이럴 경우에는 Linear Classification 을 사용할 수 없다.

 

L1 distance와 L2 distance, NN, KNN, Linear Classification에 대한 코드도 담으려 했으나 따로 정리해서 올리는게 나을 것 같다.