Stanford의 유명 강의인 cs231n을 수강하고 정리한 글이다.
해당 강의는 유튜브에서 무료로 볼 수 있다.
3강 -
https://www.youtube.com/watch?v=h7iBpEHGVNc&t=2096s
오늘은 3강인 Loss Functions and Optimization에 대해 정리해 보려 한다.
✏️ Recall
- 저번 시간에 KNN 알고지름과 Linear Classification 에 대해 알아보았다.
- 예시에서는 W (가중치) 값을 랜덤으로 정해놔서 정확도가 떨어졌었는데 이를 해결하기 위해 W값을 정해야한다.
- 그렇다면, W값은 어떻게 정할까?
✏️ Loss Function

- 직전 강의에서 나왔던 예시이다. 고양이는 자동차로 인식하였고, 개구리 또한 자동차로 인식한 것을 볼 수 있다.
- 여기서 자동차만이 정답을 맞췄다. 정확도가 많이 떨어지는 모습을 볼 수 있다.
- 이제 Loss값이 등장한다. Loss값은 얼마나 정답에서 멀어졌는지를 알려주는 값이라고 할 수 있다.

- 그리고 그 오차값을 구하는 함수가 Loss Function 이다. 위 사진을 보면
- xi 는 이미지이고 yi는 레이블이다. 그리고 오차값 L은 f(xi,W)라는 Linear Classification Function의 결과와 yi를 오차함수인 Li에 넣어 나온 값의 평균이라고 볼 수 있다.

- 그렇다면 대표적인 오차 함수인 SVM Loss를 확인해보자
- 밑의 수식을 간단하게 해석하여 작동하는 방식을 알아보자
- if . j == yi 라면 즉, 정답 레이블이면 넘어간다. (계산하지 않음)
- if 정답 레이블이 아니면, sj+1이 syi보다 작거나 같으면 넘어간다. (0으로 계산)
- 위의 경우가 아니라면 sj - syi + 1을 오차값에 더한다.
- 모든 레이블을 돌면 최종 오차값이 나온다.
- Q. 왜 syi >= sj + 1인가?
- 우선 syi >= sj 인 이유는 정답 레이블을 빼고 계산하기 때문이다. 정답 레이블이 아닌 경우 syi보다 sj가 더 작아야하는게 맞다. (정답이 아니므로 syi보다 작은 값이 나올 수록 좋다.)
- +1을 해주는 이유 : 단순하게 syi >= sj 로 설정할 경우 정답 score와 sj score이 굉장히 비슷해도 오차가 0으로 계산될 수 있다. 이는 그렇게 좋은 상황은 아니며 그것을 방지하기 위해 +1을 해줘서 방지하는 것이다. '이정도는 차이가 나야 옳게 학습이 된것' 이라고 생각하는 것이다. (개와 고양이 분류를 할때 개 점수 : 5.3 고양이 점수 5.2의 경우는 좋지 않다. 개 점수 : 5.3 고양이 점수 : -3.0 이 좋은 경우이기 때문)

- x축이 syi (정답 이미지 점수) 이고, y축이 오차값인 그래프로 그려보면 이런 그래프가 나온다. 이를 "Hinge Loss"라고 부르기도 한다.
- sj에서 + 1을 하는 순간부터 loss값은 0이 된다.
- syi가 -로 갈수록 loss값이 늘어나는 것을 볼 수 있다.

- 다음은 예시에서의 계산이다. 고양이의 정답값인 syi는 3.2 자동차의 정답값인 sj는 5.1이기 때문에 max(0,5.1-3.2+1)을 계산한 것과 같은 방식으로 개구리의 정답값으로 대입해보면 2.9가 나오게 된다. 그러면 Li (L(고양이))의 Loss값은 2.9가 나오게 된다.
- 전부 다 구해서 (L(고양이), L(개구리), L(자동차)) 평균을 계산하게 되면 최종 Loss 값을 구할 수 있게 된다.
- 수업에서 다양한 질문이 나왔다.
- Q. 정답 score까지 다 더한다면 어떻게 되나요?
- A. max(0, sj-syi +1)인데 sj = syi가 되므로, 1이 더 나오게 된다. 이러면 최소값 또한 1이 되는데, 별 의미는 없지만 최소값이 0인것이 더 낫다고 한다.
- Q. score의 합이 아닌 평균을 구한다면?
- A. 상관없다. 이는 단순한 re-scaling 에 해당된다.
- Q. Loss 값들을 제곱하면?
- A. 이건 상관있다. Loss값은 얼마나 잘못되었는지를 측정하는 도구인데, 제곱하면 그 값이 엄청나게 커진다.
- Q. Loss가 0이 되게 하는 W를 찾았다. 이는 유일한가?
- A. 유일하지 않다. 그리고 W를 두배한 2W 또한 Loss가 0이다.
- Q. Loss가 0이면 제일 좋은것인가?
- A. 아니다. 이상한 말이지만 0은 그렇게 좋지않다. 왜냐하면 우리는 training set을 고려중이다. 근데 실제로 test set을 사용하기 때문에 0이 된다는 것은 과적합 (overfitting)이 일어났다고 생각된다.

- 그래서 과적합 방지를 위해 Regularization 이라는 방법을 사용한다. 위 함수를 보면 Loss Function 의 계산식에 람다*R(W)가 추가된 것을 볼 수 있다.
- 이는 더 단순한 W를 선택하는 것인데, 여기서 오컴의 면도날이라는 용어가 나온다.
- 오컴의 면도날 : 다양한 가설을 가지고 있고, 모든 가설이 현상을 설명할 수 있다면 가장 단순한 것을 선택하라.
- 이는 일종의 패널티를 가해서, Classifier를 최대한 간결하고 심플하게 만들어준다.
- 람다값은 hyperparameter에 해당하는데 람다가 너무 강하면 너무 심플해지고, 너무 약하면 하는 의미가 없어진다.

- 예시에서는 R(W)가 L2 Regularization 일 경우 w1과 w2에 대해 점곱(dot product)를 했을 때, 1이라는 값이 나옵니다.
- 잠시 dot product에 대해 짚고 넘어가자면 벡터의 내적이다. 즉 간단하게는 벡터 곱이라고 할 수 있다.
- 이는 두 가중치가 loss값이 같다고 할 수 있습니다. 이떄, L2와 L1 Regularization은 어떤 W를 선호하는지 확인해보면
- L2의 경우 W2를 선택한다. 그 이유는 w값이 최대한 평평하게 (균등), 너무 큰 값이 없이 비슷하게 만들고 싶어한다. 또한, 가중치의 값을 정확히 0으로 만들지는 않는다.
- L1의 경우 W1을 선택한다. L1은 0의 개수에 따라 복잡도가 정의되기 때문에, 0이 많은 것을 선호. 또한 가중치의 값을 정확히 0으로 만들 수 있다.
- 나중에 따로 또 정리해봐야할 것 같다.

- 다음은 SVM이 아닌 Softmax Loss에 대해 나온다. Softmax는 위 사진처럼 score에 exp (지수) 제곱을 해주고 정규화를 시켜 확률로 만들어 주는 것이다.
- 위 예시에서는 cat일 확률이 0.13, car일 확률이 0.87 forg일 확률이 0.00이 된다. 당연히 확률이므로 더하면 1이된다.
- 여기서 우리는 오차값을 구하는 중이니 -log함수를 씌워준다. 그러면 작은 값이 커지고 큰 값이 작아진다.
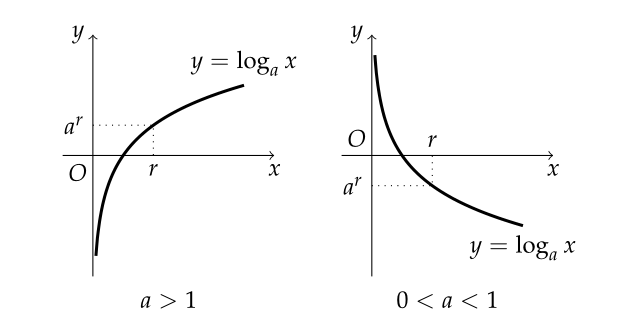
- 예시를 위해 로그함수 그래프를 추가한다.
- 그러면 cat일 확률을 낮게 잡았으니 loss값은 높아진다
- Q. Softmax의 최대, 최소값은?
- A. 최대 무한대, 최소 0이다. (내생각에 -log(1) = 0, -log(0) = 무한대 이기 때문이라고 생각했음)
- Q. Loss가 0이 되려면 실제 score는 어떤 값이여야 하는가?
- A. 자 위의 예시에서 -log(1) = 0이였다. 그럼 즉 e^syi / sum(e^sj) = 1이 되어야하며, e^syi = sum(e^sj)가 된다. 내가 이해한 바로는 syi (정답 score)은 거의 무한대값이 되어야하고 나머지 score은 -무한대에 가까운 매우 작은 값이 되어야한다. 그렇다면 score는 무한대에 가까운 값이 되어야하며, 이는 불가능에 가깝게 된다.
- 그래서 결국 softmax의 loss는 0이 나오는 일이 사실상 없을 것이다.
- Q. s가 모두 0 근처에 있는 아주 작은 수라면?
- A. s가 0근처의 아주 작은 수라면 e^s는 1에 근사할 것이다. 그러면 이를 softmax 식에 대입하면 -log(1/1+1+1+..1) 이 된다. 이는 곧 -log(1/C) 가 되며 C는 클래스 (레이블)의 개수일 것이다. 고로 log(C)가 된다.
- 이는 디버깅 할때 사용할 수 있으며, 초기에 s가 0근처의 값일 때 log(C)가 아니라면 문제가 있는 것
- Softmax vs SVM
- SVM은 +1과 같은 기준이 되는 값을 더했을때 보다 작으면 신경쓰지 않는다. 그러므로 loss가 0이 나오면 사실상 함수의 역할이 끝난다.
- 하지만, Softmax는 계속해서 loss가 0이 되기 위해 작동할 것이다. 하지만 0이 되는 일은 없으므로, 계속해서 확률을 높이려고 노력할 것이다.
✏️ Optimization
- 지금까지는 W를 '평가' 하는 손실함수와 그것을 조정해주는 regularization에 대해 알아보았지만, W를 어떻게 구하는지는 알지 못했음 이번 Optimization은 그것과 관련된 이야기이다.
- Optimization 에 대한 비유로 수업에서는 눈을 가린 상태로 산을 내려오는 상황을 가정한다.
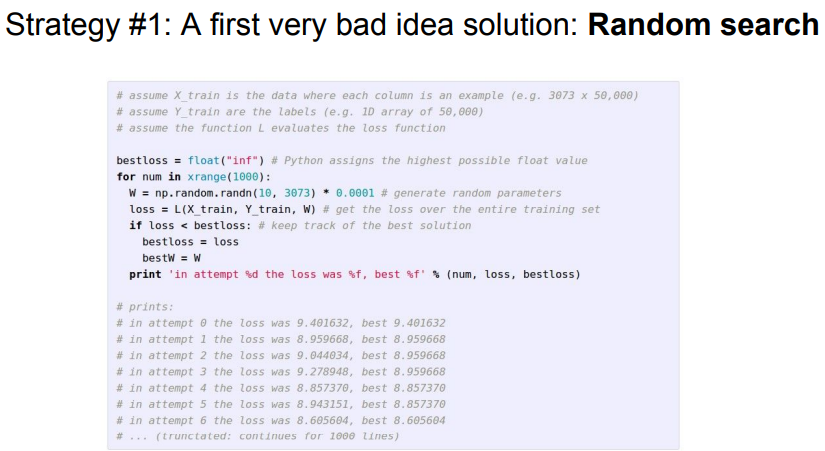
- 산을 내려가기 위한 가장 안좋은 방법은 랜덤으로 내려가는 것이다.
- 위 예시 코드의 정확도는 15.5%인데, SOTA(State Of The Art)가 95%임을 감안하면 굉장히 낮은 수치이다.

- 두번째는 경사를 따라가는 것. 즉 경사가 더 낮은 곳으로 이동한다. 위 수식은 미분의 정의로 고등학생때 봤던 것 같다.
- 미분이 '기울기'를 구하니까 산의 '기울기'를 따라 내려온다고 할 수 있다. (간단히는)

- 그래서 위 사진처럼 현재 W(가중치)의 첫번째 값에 h를 더해서 (여기서는 0.0001) 그것을 미분을 하면 -2.5라는 기울기가 나오게 된다.

- 이번에는 두번째 값에 더해서 미분을 했더니 0.6이라는 양수 기울기가 나왔다.
- 0.0001 씩 더해가며 계산하는 것은 생각보다 오래걸리기에 비효율적이다.
- 그래서 그냥 미분 공식을 사용하는 방법도 있다.
- Numerical gradient : 대략적임, 느림, 작성하기 쉽다. (위 식으로 계속 적용)
- Analytic gradient : 빠르고, 정확, 작성하기 어렵다. (그냥 미분 공식으로 계산)
- 결론 : 미분을 해서 loss가 하강하는 방향으로 진행한다.

- 경사 하강법의 sudo 코드인데 여기서 weights_grad 에서 미분을 진행하고, step_size를 곱해주는데 step size는 Learning rate라고도 하며, 실제 학습시 정해주어야 한다. 이는 -gradient 방향으로 얼마나 내려가야 하는지를 나타낸다. (너무 멀리 가버리면 엉뚱한 곳으로 매우 멀리 갈 수 있다.)
- 또한, 모든 데이터를 이렇게 계산하기에는 너무 오래 걸린다. 그래서 Stochastic Gradient Descent (SGD)이다.
- loss 계산시, training set에서 일정 minibatch (보통 2의 승수 32,64,128...)을 구성해서 추정치를 계산한다.
- 결론은 Loss 값을 구해서 정답과 얼마나 멀어졌는지 알 수 있는데 SVM, Softmax 가 존재하고
- 과적합 방지를 위해 Loss 계산에서 R(W) 라는 Regularization 함수를 추가한다.
- Loss가 줄어드는 적절한 가중치를 구하기 위해 Optimization을 하는데 이는 경사 하강법으로 한다.
- Stochastic Gradient를 써서 미니 배치 방식으로 loss값을 추정한다.
- 밑 슬라이드에서 이미지 특징에 대해 나오는데
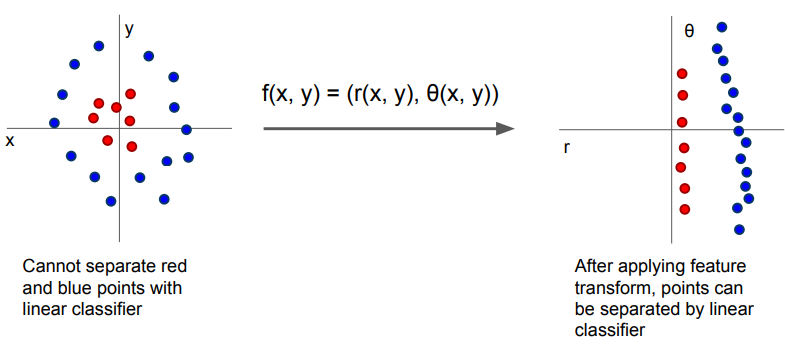
- 위 사진 처럼 하나의 선으로 분류할 수 없는 점들을 극좌표 변환을 통해 하나의 선으로 분류할 수 있게 만드는것에서 이미지 특징 추출에 영감을 얻었다
- 그래서 이미지를 색별로 나누는 Color Histogram, 이미지의 기울기 특징을 추출하는 Histogram of Oriented Gradients (HoG), NLP 기술에서 영감을 받아 이미지를 나누어 군집화 한 후 각도 혹은 색들을 추출하여 이걸 저장해놓고 새로운 이미지와 비교하는 Bag of Words 등의 방법이 존재한다.
- 5~10년 전만 해도 이런식으로 특징을 직접 추출했는데, CNN을 이용하면 그런 특징을 알아서 추출해준다는 내용이였다

